Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
PDF) A method for proving Ramanujan series for 1/π
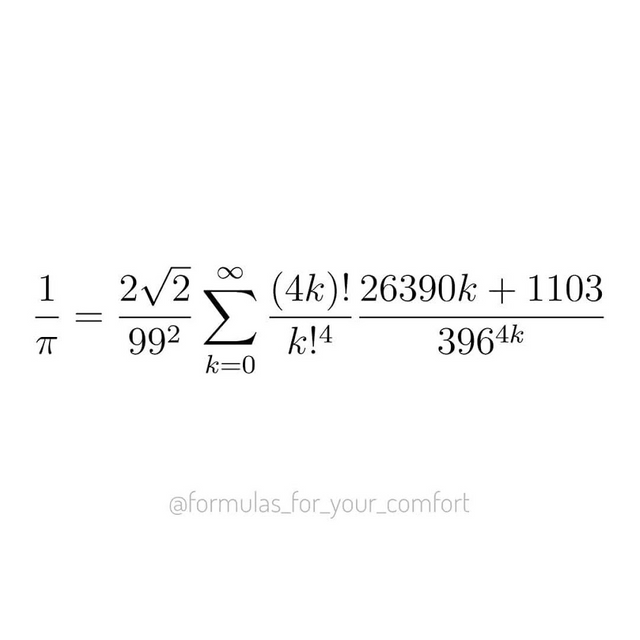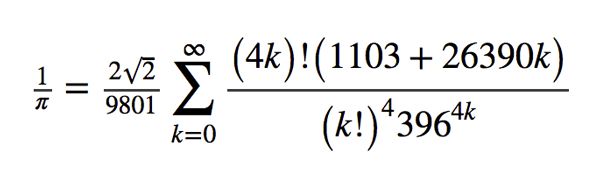
Joseph T Noony on Twitter: "Ramanujan's formula and its variants are today used by supercomputer algorithms for calculating pi correct to millions of decimals of accuracy! What a true genius he was
Extra-math - An identity derived from Ramanujan between π,... | Facebook
0027: Part 6, Ramanujan's pi formulas and the hypergeometric function - A Collection of Algebraic Identities
Tamás Görbe on Twitter: "@fermatslibrary This is the Ramanujan-Sato series found by Ramanujan in 1910. It computes a further 8 decimal places of π with each term in the series. The first
Pi Table with Ramanujans,Chudnovsky Formulas
Ramanujan–Sato series - Wikipedia
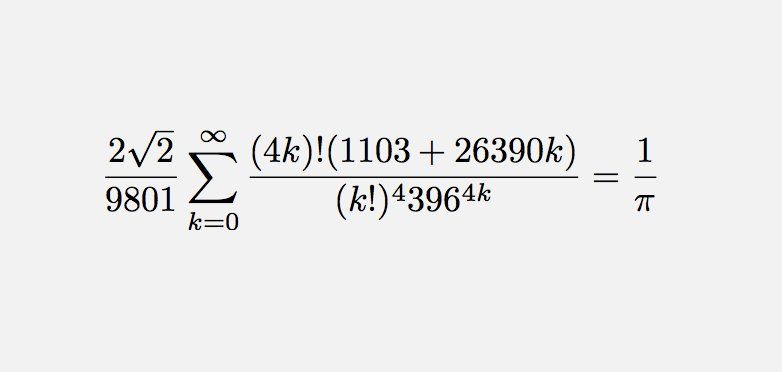
Fermat's Library on Twitter: "Ramanujan discovered this peculiar way to represent 1/π. https://t.co/nyge5IeqFM" / Twitter
円周率π The Ramanujan Pi Formula+1000digits #002|デザインTシャツ通販【Tシャツトリニティ】
0016: Article 6 (Ramanujan's Pi formulas) - A Collection of Algebraic Identities
Ramanujan's Identities
Ramanujan's Strange Formula for Pi - Wolfram Demonstrations Project
Ramanujan-like formulae for $$\pi $$ and $$1/\pi $$ via Gould–Hsu inverse series relations | SpringerLink
0027: Part 6, Ramanujan's pi formulas and the hypergeometric function - A Collection of Algebraic Identities
National Geographic India - #DidYouKnow that one of these infinite series was used to calculate pi to more than 17 million digits? This #NationalMathematicsDay, let's celebrate one of the world's greatest mathematicians,
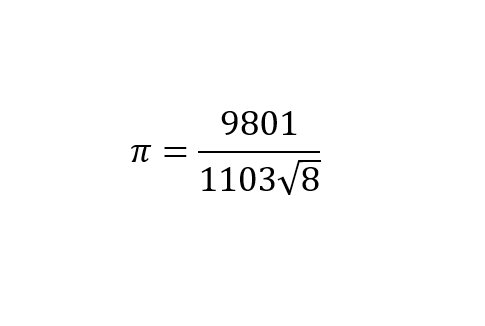
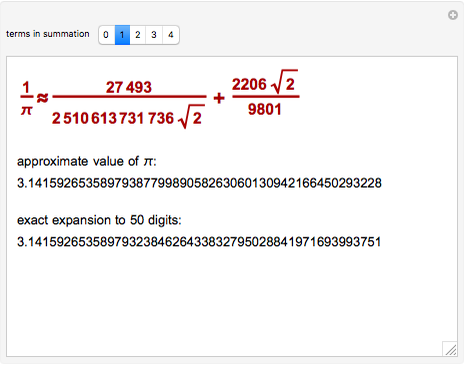
![PDF] On the elegance of Ramanujan's series for $\pi$ | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/18b60f85d381d093d696660cff44f90145509dfa/6-Table1-1.png "PDF] On the elegance of Ramanujan's series for $\pi$ | Semantic Scholar")
PDF] On the elegance of Ramanujan's series for $\pi$ | Semantic Scholar
0019: Article 9 (More Pi Formulas) - A Collection of Algebraic Identities
Extra-math - 📊Ramanujan Pi-Formula & Derivation | Facebook
![Happy Pi Day 2020! The Srinivasa Ramanujan Series | Python [ITA] - YouTube](https://i.ytimg.com/vi/ri7twYfBckQ/hqdefault.jpg "Happy Pi Day 2020! The Srinivasa Ramanujan Series | Python [ITA] - YouTube")
Happy Pi Day 2020! The Srinivasa Ramanujan Series | Python [ITA] - YouTube
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
A monstrous formula : Ramanujan's approximation of pi — Steemit
Solved Ramanujan's Formula for Pi First found by Ramanujan. | Chegg.com
Ramanujan: He who had the Pi & ate it too! | The Crooked Pencil
Who Was Ramanujan? | Mathematics, Start writing, Writing
